BLOQUE 1 DISEÑAS Y ELABORAS ALGORITMOS PARA LA SOLUCIÓN DE PROBLEMAS
Empezaremos por definir y entender que es un problema. La palabra como tal se refiere a una determinada cuestion o asunto que requiere solución. Se trata de algún asunto en particular, que en el momento en que se solucione aportara beneficios. Es una situación que nos impide lograr que un objetivo, una condición mental que impide llegar al satifactor. En matemáticas es muy común este tipo de pasos para llevar a la solución de un objetivo, ya que esta muy relacionado también con la informática, pues aquí se manejan algoritmos.
En términos mas precisos PROBLEMA: Es una cuestión que se plantea para hallar un dato desconocido a partir de otros datos conocidos, o para determinar el método que hay que seguir para obtener un resultado dado.

Metodología para la solución de problemas
Antes de hablar de metodologías de solución de problemas debes tener muy claro el concepto de método, que a lo largo de la historia ha llamado la atención de gran cantidad de filósofos y científicos. El Diccionario Larousse define el término método como "el conjunto de operaciones ordenadas con que se pretende obtener un resultado". La metodología es la ciencia que aplica este método. Existen muchos tipos de metodologías, como la metodología de investigación, metodología de enseñanza-aprendizaje, etc., así como la metodología de solución de problemas, que aplicamos constantemente en la vida diaria. Pero en este caso hablaremos específicamente de la solución de problemas que podemos resolver mediante el uso de la computadora.
La resolución de los problemas consta de cinco etapas que garantizan la llegada correcta a la solución: identificación del problema, planteamiento de alternativas de solución, elección de una alternativa, desarrollo de la solución y evaluación de ésta.
1. Identificación del problema
La identificación del problema es una fase muy importante en la metodología, pues de ella depende el desarrollo ulterior en busca de la solución. Un problema bien delimitado es una gran ayuda para que el proceso general avance bien; un problema mal definido provocará desvíos conceptuales que serán difíciles de remediar posteriormente. En esta etapa es fundamental el análisis de la información inicial (entrada) con el fin de distinguir los datos pertinentes de los que no lo son, de manera que se pueda elegir la configuración más conveniente respecto a las soluciones posibles. También deben definirse los datos de salida que garanticen la continuidad del proceso para que sea más fácil eliminar las expectativas negativas.
2. Planteamiento de alternativas de solución
Después de la definición del problema y del análisis de los datos de entrada, el proceso continúa con el análisis de las alternativas de solución. Por lo general, la solución de un problema puede alcanzarse por distintas vías. Es útil tratar de plantear la mayor cantidad de alternativas posibles de solución, pues de esta forma las probabilidades aumentan a favor de encontrar la vía correcta. Se debe destacar que no es conveniente extender demasiado el número de alternativas, pues si el número de éstas es demasiado alto, se presentará una mayor dificultad para elegir la mejor de todas, que es en definitiva el objetivo del proceso.
3. Elección de una alternativa
Después de tener todo el repertorio de alternativas, es necesario pasar a otra etapa: la elección de la mejor entre todas las posibilidades. Esta fase es muy importante porque de la elección realizada depende el avance final hasta la solución. La orientación hacia delante supone la irreversibilidad si la decisión es acertada o una "reversibilidad onerosa", pues si la decisión no es acertada, es necesario retroceder, lo que afecta la "optimidad" del proceso.
Por lo tanto, es necesario que cada alternativa sea bien analizada para que la toma de decisiones sea bien justificada. Deberás elegir la alternativa que sea la más adecuada para la solución del problema, tomando en cuenta las características del problema y las características que deberá tener la solución, así como los elementos, datos o información con la que cuentas.
4. Desarrollo de la solución
Después de decidir cuál es la mejor alternativa de todas, se llega a la etapa de la solución. En esta fase, a partir de los datos relacionados con la alternativa seleccionada, se aplican las operaciones necesarias para solucionar el problema. La selección de los procesos también debe ser determinada en función de la optimidad, es decir, las operaciones deben llegar a la solución por el camino más corto para garantizar la mayor eficiencia en el funcionamiento. Si la alternativa es la óptima, llevará a la solución deseada que fue prevista en la identificación del problema.
5. Evaluación de la solución
Luego de haber desarrollado la solución queda aún una etapa, que es la evaluación. En los procesos industriales a este procedimiento se le llama control de la calidad y consiste en determinar que la solución obtenida 'es lo que se esperaba conseguir comprobando que el resultado sea correcto. En esta fase se deben "pulir" los procesos ya realizados y tratar de llevarlos a un grado mayor de optimidad, pues el algoritmo más eficiente en la solución de un problema es el que llega a su objetivo final con la mayor economía de procedimientos que sea posible. A continuación, puedes observar un ejemplo de la aplicación de la metodología a la solución de un problema simple. Es importante saber que los problemas complejos también se resuelven con esta estructura.
Observa el siguiente video.
www.youtube.com/watch?v=5sbBuCDPZeU
Algoritmos
CARACTERÍSTICAS DE UN ALGORITMO: Todo algoritmo debe tener las siguientes características:
- 1. Debe ser Preciso, porque cada uno de sus pasos debe indicar de manera precisa e inequívoca que se debe hacer.
2. Debe ser Finito, porque un algoritmo debe tener un número limitado de pasos.
3. Debe ser Definido, porque debe producir los mismos resultados para las mismas condiciones de entrada.
4. Puede tener cero o más elementos de entrada.
5. Debe producir un resultado. Los datos de salida serán los resultados de efectuar las instrucciones.
PARTES DE UN ALGORITMO: Todo Algoritmo debe tener las siguientes partes:
· Entrada de datos, son los datos necesarios que el algoritmo necesita para ser ejecutado.
· Proceso, es la secuencia de pasos para ejecutar el algoritmo.
· Salida de resultados, son los datos obtenidos después de la ejecución del algoritmo.
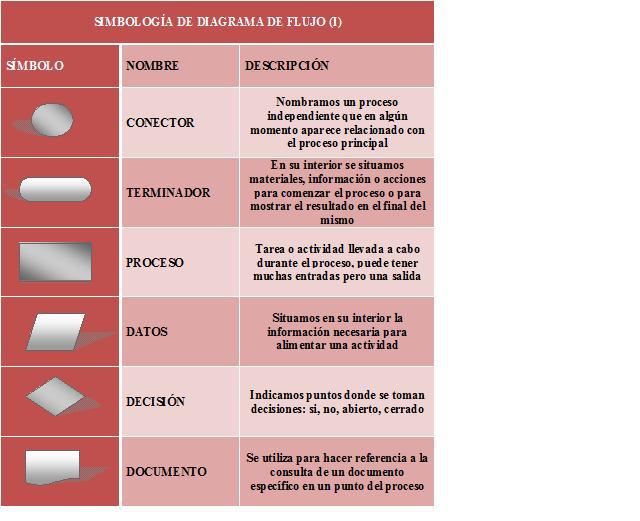
Diagrama de flujo
EJEMPLO
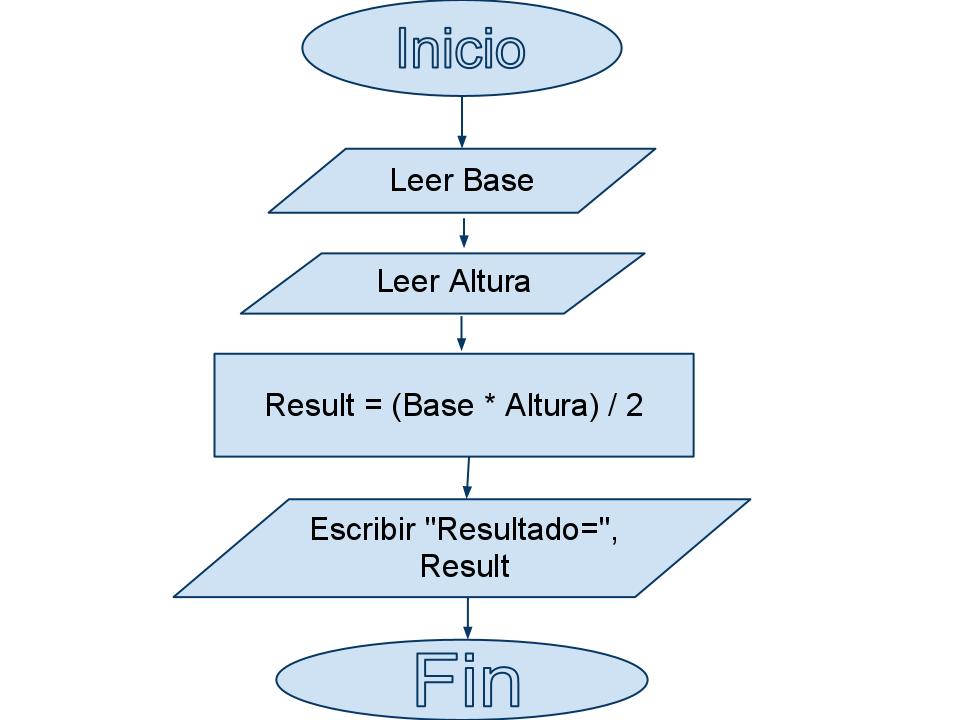
1. Calula el àrea de un tringulo
Aplicando la metodología para la solución de problemas
Aplicando un algoritmo
Creando el diagrama de flujo